[Work Log] Work Log
Training epipolar prior.
Fixing local prior using parameters learned yesterday. The computing the epipolar and full prior is more computationally intensive, since it involves twice as many dimensions. To mitigate, I eliminated every other point from the data.
Without the epipolar prior, the data likelihood is:
Log-likelihood (baseline) = -2471.12
Fixing euclidean scale and variance to zero, I trained the epipolar variance:
Log-likelihood = -2395.05
training_result =
epipolar_variance: 4.39
By allowing some euclidean-correlated variance, the iid variance should be able to drop a bit. Fixing euclidean scale to 1/1002, I trained epipolar_variance and euclidean_variance jointly:
Log-likelihood = -2394.88
training_result =
epipolar_variance: 4.3214
euclidean_scale: 1.0000e-04
euclidean_variance: 0.0335
Now training all three:
Log-likelihood = -2394.57
training_result =
epipolar_variance: 4.2877
euclidean_variance: 0.0458
euclidean_scale: 2.1581e-06
Now training all 10 parameters together:
Log-likelihood = -1294.59
training_result =
epipolar_variance: 4.2877
euclidean_variance: 0.0458
euclidean_scale: 2.1581e-06
noise_variance: 0.0821
geodesic_variance: 193.9141
geodesic_scale: 0.0031
branch_linear_variance: 0.0800
branch_const_variance: 6.1725
linear_variance: 0.1561
const_variance: 685.7670
...but we actually want noise_variance to be fixed to 1. Repeating previous run with noise_variance=1 results in:
Log-likelihood = -2381.29
training_result =
epipolar_variance: 4.2877
euclidean_variance: 0.0458
euclidean_scale: 2.1581e-06
noise_variance: 1
geodesic_variance: 33.6972
geodesic_scale: 0.0011
branch_linear_variance: 0.1028
branch_const_variance: 6.9943
linear_variance: 0.0737
const_variance: 1.8641e+03
running for 30 more iterations:
ll = 2376.76
epipolar_variance: 4.2877
euclidean_variance: 0.0458
euclidean_scale: 2.1581e-06
noise_variance: 1
geodesic_variance: 160.7604
geodesic_scale: 5.3712e-04
branch_linear_variance: 0.1028
branch_const_variance: 6.9943
linear_variance: 0.0835
const_variance: 2.1123e+03
The fullly trained model is then:
epipolar_variance: 4.2877
euclidean_variance: 0.0458
euclidean_scale: 2.1581e-06
noise_variance: 1
geodesic_variance: 15.9174
geodesic_scale: 0.0019
branch_linear_variance: 0.0485
branch_const_variance: 3.7438
linear_variance: 0.0348
const_variance: 685.7670
The samples from this prior look very nice:
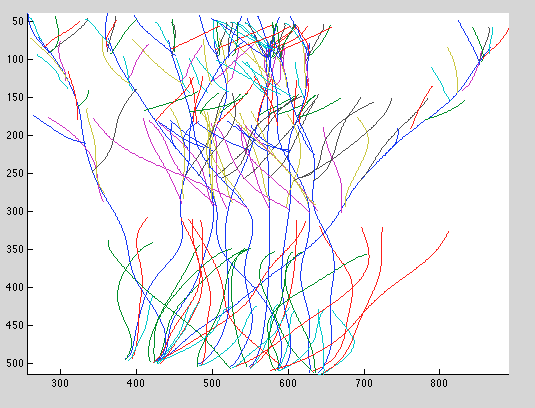
Motion is restricted to be near the epipolar lines, and the resulting curves remain smooth.
Matlab says only 314 out of 3766 are nonnegligible.
Posted by Kyle Simek